What are Exponents and Powers? Definitions, Rules, and Examples
Exponent and Power in Mathematics: Definition, Rules, and Differences
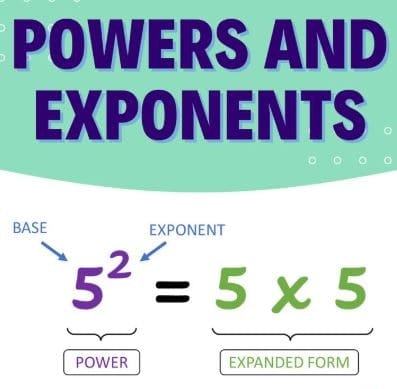
Exponents and powers are perhaps the most fundamental concepts found in mathematics, which has made it easy to get the same number multiplied times over again. An exponent is how many times that number, known as a base, is multiplied to itself. For instance, in (2^3), the number 2 is the base, and the exponent (power) being 3 shows that this number, 2 is multiplied by itself three times (same base) i.e. (2 times 2 times 2 =8). The result obtained from such multiplication is power. The result obtained from such multiplication is referred to as the power. These concepts are vital in understanding the difference between exponential and power functions and their applications in mathematics, from basic arithmetic to advanced algebra and scientific calculations. Mastering the rules of exponents and powers is crucial for solving equations, simplifying expressions, and efficiently addressing real-world problems. This ensures that calculations are devised and executed streamlined and simplified.
Exponents and powers are mathematical tools that make writing and calculating repeated multiplication of the same number easy.
Let's break it down step by step to better understand powers and exponents with important rules.
What is an Exponent and Power?

An exponent is the number written above and to the right of another number. It tells us how many times the base number is multiplied by itself. The exponent tells how many times a number is multiplied by its power.
For example, (2^3) (read as two raised to the power of 3) means (2 times 2 times 2 = 8).
Here, 3 is the exponent of a number.
2 is the base (the number being multiplied).
3 is the exponent (the number of times 2 is multiplied by itself).
A power is defined as the result of using an exponent.
For example, In (2^3 = 8), the number 8 is the power. The power rule is the base number raised to the power 3.
So, when we write (3^4), it means 3 times 3 times 3 times 3 equal 81
Here, 81 is the power. Therefore, it represents repeated multiplication.
Rules of Exponents
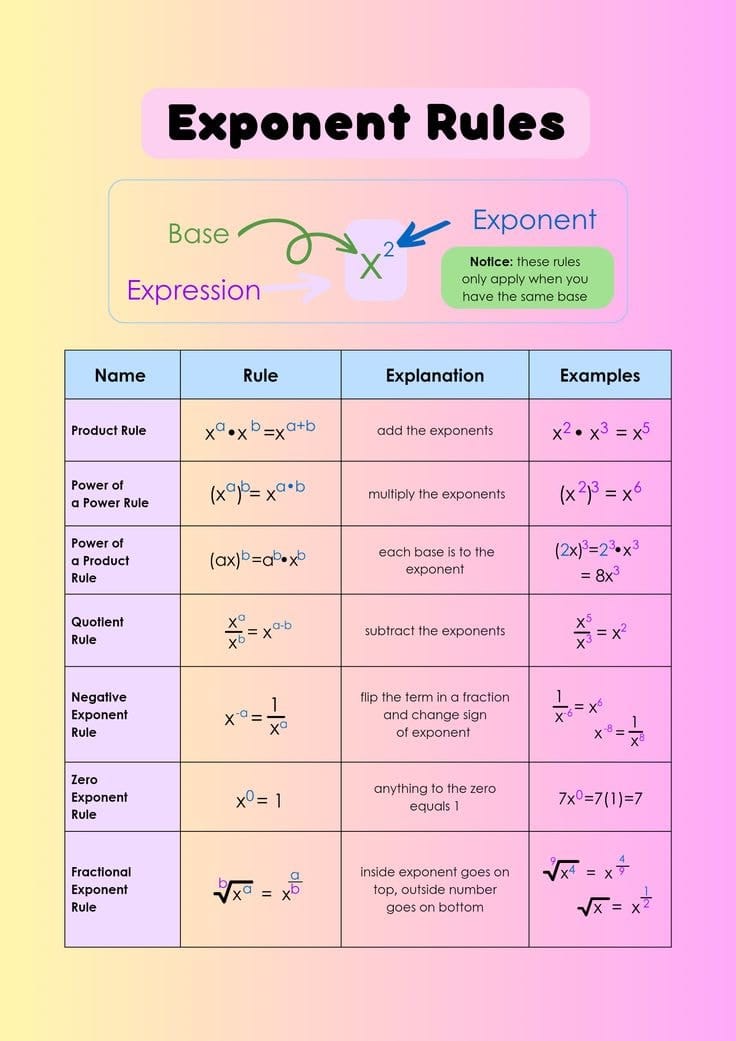
Understanding the rules of exponents enables us to work with them easily. Here are some of the most important ones:
Multiplying Powers with the Same Base: When multiplying numbers with the same base, add the exponents. a^m times a^n = a^{m+n}
Example: (2^3 \times 2^2 = 2^{3+2} = 2^5 = 32).Dividing Powers with the Same Base: When dividing numbers with the same base, subtract the exponents. a^m div a^n = a^{m-n}
Example: (5^4 div 5^2 = 5^{4-2} = 5^2 = 25).Power of a Power Rule:
When raising a power to another power, multiply the exponents.
\\[
(a^m)^n = a^{m \times n}
\\]
Example: \\((3^2)^3 = 3^{2 \times 3} = 3^6 = 729\\).Zero Exponent Rule:
Any number raised to the power of 0 is always 1 (except 0 itself).
[a^0 = 1]
Example: \(4^0 = 1\).Negative Exponent Rule: The negative exponent means the reciprocal (or the "flipped" version) of the base raised to the positive exponent.
[ a^{-n} = \frac{1}{a^n}]
Example: (2^{-3} =frac{1}{2^3} = frac{1}{8}).
Why Are Exponents and Powers Useful?
Exponents and powers help us compactly express large or small numbers. For example:
- The large number 1,000,000 can be written as (10^6).
- The tiny number 0.00001 can be written as (10^{-5}).
Exponents and powers are also used in sciences to calculate growth, in computing to measure speed or storage, and in geometry to calculate area and volume.
What Is an Exponent and Power?
An exponent of a number shows how many times a number, called the base, is multiplied by itself. When we use exponents, we write a small given number above and to the right of the base. This small positive number is called the exponent.
Example:
2^3 = 2 · 2 ·2 = 8 (mathematical expression)
2 is the base.
3 is the exponent- it tells us how many times to multiply the base by itself. (third power)
8 is the value-the result of multiplication. (number expressed after the second power of rule)
Real-Life Examples
Following are the real-life situations which involve exponents and power exponents exponent.
Doubling Bacteria Growth
Imagine one bacterium doubles every hour. By the end of 3 hours, the cumulative total number of bacteria is:
Expression: [2^3 = 2 times 2 times 2 = 8]
Such exponents make the multiple growths easily computable.
It can also be used to ascertain the pH scale.
Square Area
In finding the area of a square with a side length of 4, we multiply the side by itself:
[4^2 = 4 times 4 = 16]
Large Numbers in Science
In astronomy, the distance from Earth to the Sun is roughly (1.5 times 10^8) kilometres. That's a lot more concise than 150,000,000 kilometres.
Why Does It Matter To Know Exponents and Powers?

Exponents and powers make calculating easier because you don't have to write the number down multiple times, especially with big or repeated numbers. You can use a shorthand. It makes working with significant numbers in science, engineering, or even simple applications like calculating interest or energy usage is much easier.
For instance:
- Instead of multiplying 10 x 10 x 10 x 10 to get 10,000, you write 10^4, which stands for 10,000.
Now with exponents and powers under your belt, you are going to solve problems fast and be innovative and discover patterns in math.
Difference Between Exponent and Power Functions

Exponents and powers are two closely related mathematical functions often used in the same context, yet with different meanings and purposes of application. Each term must be defined and considered in its application to understand their differences.
An exponent rule is called a small number placed above and to the right of a base number to indicate how many times to multiply the base by itself. Exponents important rules are meant to be practised timely.
A power is called as the result of that multiplication. In other words, the exponent is the instruction, and the power is the result. It can also be regarded as a superscript number. It is mentioned up right the number.
For instance, in (3^4 = 81), 4 is the positive exponent part, 3 is the base, and 81 is the power. Exponents focus on the repeated multiplication process. It is repeated multiplication with the same factor. Hence, the correct answer is 81.
They tell us how often the base number is used as a factor. For example, in \\(2^5\\), the exponent 5 instructs us to multiply (2 \\times 2 \\times 2 \\times 2 \\times 2 = 32\\). This process of repeatedly multiplying is the key to understanding how exponents work.
Exponents are, therefore, an operation, such as addition or multiplication, that indicates "how many times." They do not generate the final number but rather form the means of obtaining it. Powers, on the other hand, are the product of applying the exponent to a base number. If exponents are the instructions, powers are the final answers.
For example, in (5^3), the exponent 3 tells us to multiply (5 times 5 times 5), and the power is the resulting number, 125. Powers are the quantities we interpret or use in further calculations. While exponents define the operation, powers encapsulate the completed result of that operation, making them the output of the mathematical process.
The relationship between exponents and powers is interdependent but distinct. The exponents provide a rule or structure, but the powers are the values you get from using it. It is similar to baking; an exponent offers a recipe with the number of ingredients to take (base) and the number of times to mix (exponent), but the power will be the final baked goods.
This distinction (main the difference between exponent and) is crucial in advanced mathematics, where powers often serve as the basis for further operations, such as solving equations, plotting graphs, or analyzing data trends. Understanding the distinction between exponents and powers helps students grasp the broader applications of both. Exponents simplify writing and calculating large or small numbers efficiently. Powers, being the outcomes, allow us to represent results compactly and use them in practical scenarios. For instance, calculating the rate of growth of investments, scientific measurements, or engineering problems often require the use of exponents and powers to interpret.
Although the terms are used interchangeably in more casual contexts, understanding both their distinct roles will always enrich understanding and strengthen mathematics problem-solving skills.
Exponent Vs Power
Exponents and powers are probably some of the most familiar and closely related yet unique mathematical concepts regarding their definitions, representations, and applications. An exponent is a small number that is placed above and to the right of a base number indicating how many times the base needs to be multiplied by itself, whereas a power is the outcome of that process. These may be minor, but these differences helpus understand how they are utilized in mathematical calculations and applications. There can be two exponents as well.
Definitions
An exponent is a mathematical notation that signifies repeated multiplication of a base number. For example, in the equation (2^3), the exponent is 3, directing us to multiply the base (2) three times: (2 times 2 times 2). The power, however, refers to the result of the operation. Using the same example, the power is 8, which is the outcome of the calculation. Essentially, exponents represent the process, while powers represent the final result.
Representation The representation of exponents and powers is another way to distinguish between them.
The general format for an exponent is \(a^n\), where \(a\) is the base, and \(n\) is the exponent.
On the other hand, Powers refer to the value produced upon performing the operation that the exponent indicates. In \\(3^4 = 81\\), the expression \\(3^4\\) is the base with an exponent, while 81 is the power. It is a subtle distinction in that powers are the quantities that are generated as the result of applying exponents.
Exponents make it easier to express big or repeated multiplications. We do not have to write \\(10 \\times 10 \\times 10 \\times 10\\) but instead use the expression as \\(10^4\\). Since powers are the result, they are usually used in further mathematical operations. Suppose that \\(10^4 = 10,000\\). Then we can use the power 10,000 in subsequent calculations, like calculating the total cost or measuring distance.
Definition
An exponent is a mathematical notation that signifies repeated multiplication of a base number. For example, in 232^323, the exponent is 3, which directs us to multiply the base 222 three times (2×2×22 \times 2 \times 22×2×2). A power, on the other hand, is the result of this operation. Using the same example, the power is 8, which is the outcome of the calculation. Essentially, exponents represent the process, while powers represent the final result.
Exponents can be there in the form of variables as well like m n.
Representation
The representation of exponents and powers is another way to distinguish between them. The general format for an exponent is ana^nan, where aaa is the base, and nnn is the exponent. Powers, however, refer to the specific value obtained after carrying out the operation dictated by the exponent. In 34=813^4 = 8134=81, the term 343^434 includes both the base and the exponent, while 81 is the power. This distinction emphasizes that powers are the numerical results produced by using powers and exponents together.
Usage in Simplification
Exponents simplify the expression of large or repeated multiplications. Instead of writing 10×10×10×1010 \times 10 \times 10 \times 1010×10×10×10, we can represent this as 10410^4104. Powers, being the outcome, are often used in subsequent mathematical calculations. For example, if 104=10,00010^4 = 10,000104=10,000, the power 10,000 can be applied in further computations, such as finding the total cost or measuring distance.
Examples to Demonstrate Differences
Let’s consider a few examples:
In 25=322^5 = 3225=32, the exponent is 5, instructing us to multiply 222 five times. The power is 32, which is the result.
In 53=1255^3 = 12553=125, the base is 5, the exponent is 3, and the power is 125. Here, 125 is the final numerical value after applying the exponentiation process. This is a case of larger number.
Role in Scientific Notation
Graphical Representation
Zero and Negative Exponents
Exponents also include special rules, such as zero and negative exponents. For instance, 20=12^0 = 120=1 because any non-zero number raised to the power of zero is 1.
Exponent and Power - FAQs
What are the rules of exponents?
Exponents make math shorter and easier! We can use an exponent instead of writing the same number multiplied many times. For example:
232^323 means 2×2×22 \times 2 \times 22×2×2.
Here are the basic rules of exponents:
Multiplying Powers with the Same Base
Dividing Powers with the Same Base
Power of a Power
Power of a Product
Power of a Quotient
Zero Exponent Rule
Negative Exponent Rule
What Are Negative Exponents in Maths?

A negative exponent means you flip the base to its reciprocal and change the exponent to positive.
Rule:
a−n=1ana^{-n} = \frac{1}{a^n}a−n=an1
Why are Exponents Referred to as Powers?
In mathematics, the terms exponent and power are closely related but have distinct meanings and historical origins:
Exponent: The word comes from the Latin exponere, meaning "to put forth." An exponent indicates how often a number (the base) is multiplied by itself. For example, in 232^3, the exponent is 3, meaning 2×2×22 \times 2 \times 2.
Power: The term originates from the Greek word dúnamis, which means "amplification" or "strength." Ancient Greek mathematicians, like Euclid, used it to describe the square of a line segment, referring to the area of a square. Over time, "power" evolved to describe expressions involving exponents, such as "the third power" for cubing a number.
In modern math, "power" often refers to the entire expression involving the base and the exponent. For instance, in 545^4, the base is 5, the exponent is 4, and the whole expression is called the fourth power of 5.
These terms help simplify the representation of large numbers and repeated multiplications, essential in mathematics and its applications.
What is exponent and power in math?
In math, exponent and power help show how many times a number is multiplied by itself.
The base is the number being multiplied.
The exponent is the small number written above it, telling how many times to multiply the base.
The power is the result.
For example:
23=2×2×2=82^3 = 2 times 2 times 2 = 8
Here, 2 is the base, 3 is the exponent, and 8 is the power.
What is a power function in math?
A power function is a type of math rule that uses exponents. It shows how a number grows when you multiply it several times.
For example:
If the rule is f(x)=x2f(x) = x^2, it means you take a number (xx) and multiply it by itself (like 32=3×3=93^2 = 3 \times 3 = 9).
If the rule is f(x)=x3f(x) = x^3, it means you multiply the number by itself 3 times (like 23=2×2×2=82^3 = 2 \times 2 \times 2 = 8).
Power functions help us understand patterns of growth or change in math. Think of it as a "shortcut" way to write repeated multiplication!
What are the 7 Laws of Exponents?
Following are the seven laws of exponents:
Product of Powers Rule
Quotient of Powers Rule
Power of a Power Rule
Power of a Product Rule
Power of a Quotient Rule
Zero Exponent Rule
Negative Exponent Rule
Comments
Your comment has been submitted