The Basics of Geometry: Simple Concepts for Kids and Parents
The Basics of Geometry: Simple Concepts for Kids and Parents
Geometry is an algebra of shapes connecting everyday objects such as a square table, a round clock, or a triangular traffic sign with their properties and purposes. It involves points, lines, surfaces, and shapes in two and three dimensions, helping us understand their functions. By acquiring the basics of geometry, cognitive skills such as spatial thinking, puzzle-solving, and creativity become more accessible to children and parents.
This tutorial introduces basic geometry shapes and equations. It includes foundational math concepts, shapes, and simple geometry formulas, serving as a perfect guide for kids.
In simple terms, What are the Basics Of Geometry For Kids?

Geometry is the science of shape, space, and their interaction, playing an important role in comprehending the world around us. It introduces young children to the basics of geometry with images of basic geometric shapes and concepts, such as identifying and naming simple geometric forms. These include circles, triangles, squares, and more.
A circle is a perfectly smooth shape, without curves or angles. The boundary is two points that are at the same direction and distance from the center. For example, on familiar objects, like a watch or a pizza, a circular object means that every point on the edge is the same distance from the center. This symmetry creates a smooth, continuous outline.
A triangle is a closed curve formed by three line segments. It is one of the basic geometry shapes, with three edges and three angles, which can be of any size. Because it is such a simple plane, it serves as an easily accessible primitive in the arts and architecture.
A square is one of the basic geometry shapes, featuring four equal sides and angles. All the sides and side angles are of equal length, and each angle measures 90 degrees. It is an interesting example of a symmetrical shape with equal side length.
These simplified forms are not just abstract geometrical paintings, but the foundation from which object relationships are learned, space is measured, and patterns are developed. Even when working with moving images of both two-dimensional and three-dimensional shapes, children begin to recognize the basics of geometry used in the real world, such as the rectangular window in a house, the wheel of a car, or the wall clock.
It becomes easier for kids to focus their attention on more complex characteristics, such as triangles, parallelograms, or basic geometry equations related to these shapes. By studying the principles of basic geometry shapes and their properties, they acquire analytical abilities that they can apply not only to solving middle-grade math problems but also to addressing everyday challenges and advanced mathematical problems.
How Does Geometry Work?
Geometry functions through the use of logical reasoning in the context of shape, size, and spatial position. It allows us to explore the world by understanding the basics of geometry, including dimensionality, angles, and other characteristics of a variety of geometric solids. These can range from basic geometry shapes like 2D rectangles to more complex 3D forms such as cubes.
Geometry is about measurement and relationships:
Measuring dimensions involves length, width, and height. The area of a rectangle can be calculated using length and breadth, which tells us how much space it occupies.

Calculating angles: Two lines are orthogonal (perpendicular) if their intersection is at a right angle of 90 degrees. The sum of angles in any triangle will always be 180° irrespective of the type of triangle. Angles are produced at vertices where the sides of a shape meet.
Exploring properties: Symmetry, congruency, and parallel lines are employed to describe shape relationships like lines that never move a certain distance apart or a shape that has a symmetrical visual appearance after a flip.
For example:
Calculating the surface area and volume of a rectangle can approximate the quantity of carpet necessary to cover the room.
The Circumference of the circle calculation can be done to determine the garden perimeter as the circumference of a circle.
From drawing shapes in painting to geometry basics shapes formulas basic math conversion problems to the design of a playground, to the geometry of bookcase angles, the rules of geometry bring the otherwise abstract to life and are endlessly engaging. If children master these concepts, they can see real-world basic math problems and imagine how the principles might be used in deeper and more impactful ways to understand how mathematics impacts the world around them.
How to Do Geometry: Basic Problem-Solving Steps
To solve geometry problems, kids can follow these simple steps:
Understand the problem: Identify what is being asked—like finding the area, perimeter or angles.
The next stage is the careful reading of the question, followed by identifying what the question is asking. Are you finding the area, perimeter, length, or angles? Once you understand the requirement, you can apply the basics of geometry, including lengths, widths, and basic geometry equations, to solve the problem accurately.

Visualize: Draw the shape to make the problem easier to see.
Drawing the shape or diagram is crucial. No matter if it is a rectangle, triangle or circle, the problem is easier to understand when using a well-defined image is possible. For example, if the task is about 2D shapes (squares or triangles), define the boundaries and angles so they are not confused.
Use formulas:

Geometry relies heavily on formulas to solve problems. Memorizing and applying them is key to success. Some common examples include:
Rectangle area = length × width
Triangle area = ½ × base × height
Circle circumference = 2 × π × radius
Check your work: Double-check calculations for accuracy.
Errors can occur at any point of time, so verify your results and the solutions.
Are the units correct? Does the solution match the diagram? Revisiting your work can help avoid simple errors.

Basic Mathematical Concepts Can Be Taught
Geometry is a world apart from recognizing basic geometry shapes; it is the portal to discover the patterns, designs, and structures of the world. Understanding the basics of geometry is not just a good teaching tool for developing practical problem-solving and analytical skills but also offers a means to apply basic geometry equations effectively in enhancing problem-solving abilities.
Categorization and Comparison
Categorizing shapes helps kids recognize patterns and think logically. For instance, triangles have three sides, quadrilaterals have four, and polygons are poly-sided figures. This builds their understanding of geometry step by step.
Examples of Categorization:
Polygons: Closed figure with straight sides. The triangle is composed of three lines segments drawn-line segments, and the pentagon has five-line segments.
Quadrilaterals: Polygons with four sides (rectangles, squares, etc). A rectangle has two equal opposite sides, and a square has all sides of equal length.
Triangles: Equilateral triangles have three equal sides, isosceles triangles have two equal sides, and scalene triangles have no equal sides.
Activities for Comparison:
Shape Sort: Give children of different shapes cutouts of various kinds and ask them to group in categories like 2-D and 3-D shapes.
Angle Hunt: Angles are defined using a protractor and it is determined whether an angle is right, acute, or obtuse.
Instruct students to state their observations using terms such as closed figure, right angle, and opposite angles, thereby establishing familiarity with geometric vocabulary.
Drawing with Basic Geometry Shapes
Drawing is an essential step in understanding geometry, the basic shapes of geometry shapes. It helps students visualize shapes, learn their sizes and see how they fit together.
Drawing Exercises:
Connecting the Dots: Ask kids to draw patterns different from three-dimensional shapes, like squares, triangles, and hexagons in a dotted grid. Give a task to count how many line segments and angles each shape have.
Exploring Symmetry: Fold a sheet of paper in half to investigate symmetry. Compare the left and right portions of the sheet along their constituent lines and see different shapes as they are folded. Children can recognize that each half is a mirror image, with the parallel lines and sides presenting different patterns. Are shapes like circles and squares always symmetric?
Activities should be designed to directly address the concepts of three dimensions and two-dimensional figures, thereby allowing students to establish and comprehend the meanings of the words and the related study materials concepts.
Basic Geometry Equations for High School Students
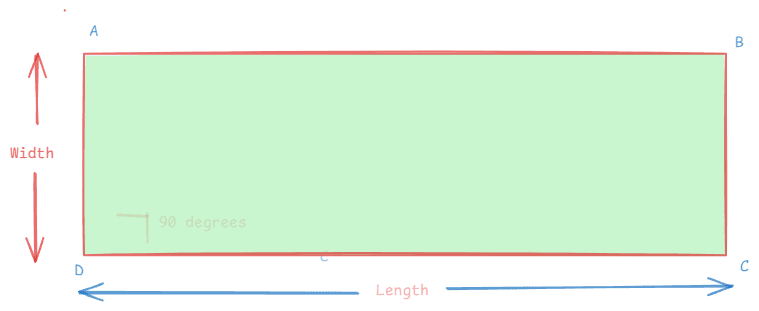
The perimeter of a Rectangle:
Perimeter = 2 x (length + width)
Example: For a rectangle with a length of 12 units and a width of 7 units then,
Perimeter =2 ×(12+7) = 38 units.
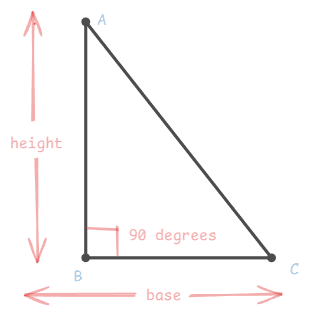
Area of a Triangle:
Area = 2 x base x height
Example: If a triangle's base is 10 units and its height is 8 units then,
Area = 2× 10 x 8 = 40 square units.
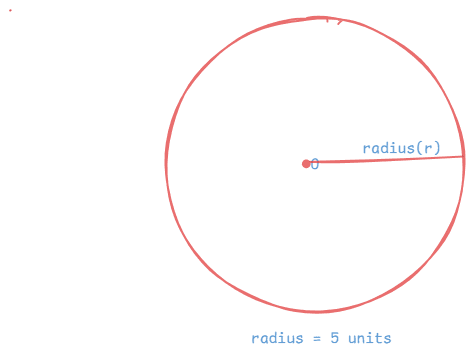
Circumference of a Circle:
Circumference = 2πr
Example: If a circle radius is 5 units then,
Circumference = 2π ×5=31.4 units (approx)
How to Explain the Basics of Geometry for Kids
Teaching basics of geometry formulas to children becomes simple when you simplify complex concepts into entertaining and meaningful ones. For instance, patterns of chessboard shapes (2D figures) and line segments belong to elementary geometry formulas. Children can easily grasp and have fun learning when the rules are presented in a logical order in a straightforward, lightweight manner.
Begin by Building Shape Knowledge
Kinds of geometrical shapes, including squares, triangles, rectangles, etc. Explain to children the word closed figures and define them in terms of the corresponding line segments and length.

Activities:
Flashcards with pictures consisting of line segments of various shapes (squares, rectangles) can be used to teach children to learn the names and properties of different shapes together. When children use flashcards, they can observe that each shape is built out of line segments, and children can understand how to recognize the sides and angles of each shape.
A triangle is a closed figure with three lines. It can be any type of triangle, such as equilateral triangles or isosceles triangles.

Shape Matching:
Match real-life objects to their geometric counterparts. A clock is a circle, a book is a rectangle, and a slice of pizza is a triangle.
These tasks ensure children can recognise and discover the basic shapes and components of 2-D shapes and establish a foundation for 3-D shape know-how in the subsequent time.
Jog Their Memory
Educate children to remember existing learning by attaching shapes to something they do once a day. It is more than a confirmation of learning; it also builds affective investment in learning.
Show them that a soccer ball is composed of hexagons or pentagons and that windows are most often aligned on all four sides, creating squares and rectangles.

Simple Questions:
Is there a shape in this room with a right angle?
Which object in the kitchen looks like a triangle?
By tying concepts together, like the images of two-dimensional points generating the line or angles between the angles and sides of each other or line segments drawn from opposite points and paired in some figures, it may be possible to make kids more aware of the hidden geometry structures and patterns.
Create a Visual Memory
Visualization is crucial for understanding geometry. With the help of appealing charts or software, the basic geometric ideas (shapes and formulas) are clearly illustrated.
Ideas for Visual Aids:
Interactive Apps: These can also be used to train a former student or a teacher on how to translate geometric shapes onto paper and determine the size and shape of the drawing.
Images of Basic Geometric Shapes: Explain the 2D and 3D geometric shapes and forms like cubes (playing cube), cuboids (matchbox), and planks (rectangular shape).
Get Them Creative with Shapes
Maintaining children's learning by visual processing of shapes as sequences into patterns or designs evokes a concrete and tangible extension of their learning. This helps them to enhance their creativity.
Creative Activities:
Shape Art: Create designs, models, or creatures using paper, clay or computer.
A house plan can be constructed with the same walls, vertices in the same plane, and isosceles roof triangles.
DIY 3D Models: Build cubes, pyramids, and cones to represent the space of three-dimensional shapes. Use two-dimensional shapes' dimensions, length, and surface area to calculate their surface area and volume formulas.
These hands-on activities confirm the association between formal terms, such as line segments or curves.

Sign Them Up for Courses
Kids can learn geometry via structured courses and lessons through platforms such as Codeyoung. These programs are visual, interactive, and tailored to different age groups, making building a strong math foundation easier.
Benefits of Signing Up for Courses:
These tutorials aim to help high schoolers solve deeper problems in algebra, geometry, and statistics/probability.

Challenge the kids to create accounts at these websites to use this lesson and research other concepts in deep geometry, such as exponents, polynomial functions, or the relation between fractions, decimals, and percentiles.
Videos Explain Concepts Better
Videos and animations make it more accessible to students to learn the pitfalls of very difficult concepts, such as calculating the angles of a triangle or the formulas for geometry, etc.
Examples of Video Content:

How to Draw Geometric Shapes: Focusing on using the instruments (e.g., rulers, protractors) to accurately construct the line segments and the points allocated to them.
Real-Life Geometry Applications: Closing outlines and lines of two points, the intersecting lines being perpendicular and inside one another, are shown as they are used in computer graphics.
Keep up with School Lessons
Overlaying with content delivered in class gives students a deep into algebra geometry concepts. Work through example practice exercises that solve middle-grade mathematics problems and increase their learning to more advanced learning materials.
Practice Tips:

Implement basic conversion computations in areas and volume such as converting units.
Problem-solving with angles is the same as with intersecting, parallel lines or 2D shapes. They have opposite points where parallel sides of the lines intersect.
Explore these ideas: two lines may have opposite points, the intersecting points may be at right angles, or two shapes with the same distance units are congruent.
Basics of Geometry - FAQs
What are basic geometry equations?
Area Formulas:
Square: Area = (side length) ²
Rectangle: Area = length × width
Triangle: Area = 1/2 × base × height
Circle: Area = π × (radius)²
Perimeter Formulas:
Square: Perimeter = 4 × side length
Rectangle: Perimeter = 2 × (length + width)
Triangle: Perimeter = sum of the lengths of all three sides
Circle (Circumference): Circumference = 2 × π × radius
Volume Formulas:
Cube: Volume = (length)³
Rectangular Prism: Volume = length × width × height
Sphere: Volume = 4/3 × π × (radius)³
Cylinder: Volume = π × (radius)²× height
What are basic geometry shapes?
Geometry begins with understanding basic shapes that are either two-dimensional (2D) or three-dimensional (3D).
Two-Dimensional Shapes (2D)
These shapes exist in only two dimensions - length and width:
Circle: An infinitely compact, closed shape in which all points are at the same distance from the centre.
Square: A quadrilateral whose four sides are equal and which has four right angles.
Triangle: Made of three-line segments (closed figure).
Isosceles Triangle: Two sides of the same length.
Right-Angled Triangle: Contains one right angle.
Rectangle: A quadrilateral whose opposite sides are of equal length and which has four right angles.
Three-Dimensional Shapes (3D)
Three-dimensional shapes add depth to length and width:
Cube: Made with squares with equal length on all sides.
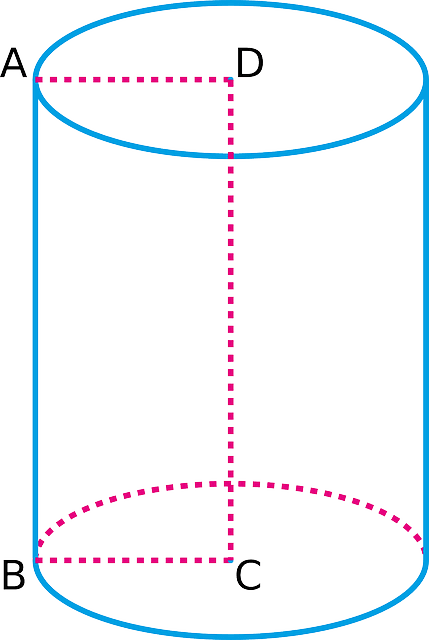
Cylinder: Made using two circles as its base and a rectangular curved surface.
Rectangular Prism: Built using rectangles with parallel sides and six faces.
What are the different types of 3D Shapes formed using rectangles and circles?
Cubes:
Formed using squares.
Each face of the cube is a two-dimensional shape (square) with equal length.

Cylinders:
Formed using two circles as the base and a curved rectangular surface.
Cylinders are common in objects like pipes, cans, and glasses.
What is Scratch math?
Scratch Math is a creative way to teach and learn math using interactive tools like Scratch. Scratch is a programming platform based on visual blocks to develop projects, making it especially engaging for middle-grades math students. The learning tool allows the students to split large mathematical problems, like word math problems, 2-dimensional figures, 3-dimensional figures, etc.
Students can learn algebraic and geometric concepts like isosceles triangles, intersecting lines and problem-solving. This method enables learning in data, statistics, probability, and some geometry principles and rules. Scratch Math offers a suitable method of teaching mathematical ideas to students in a natural way in which they develop thinking skills, problem-solving skills, etc.
How does Codeyoung teach the basics of geometry to kids?
Codeyoung makes geometric learning accessible and fun for kids. Interactive methods are employed to create account names for the geometric underlying principles, shapes, and equations to visualize the underlying concepts (e.g., line parallelism, lines and line segment length, or filled figures).
1. Interactive Tools and Activities
Using examples from the real world, like solving middle grades math solving problems
Image visualizations of two and three-dimensional figures.
2. Games and Puzzles
Geometry is enjoyable when using games, namely finding out what kind of shapes there are, finding a line sequence (which can be straight or curved), or solving problems using the two angles of a triangle.
3. Problem-Solving Challenges
Children in class take grades in mathematics by multiplying word problems into geometric formulas for area, perimeter, and volume. These challenges lead to a further explicit understanding of underlying mathematics concepts and the acquisition of analytical thinking.
4. Step-by-Step Learning
Teachers direct students first through recommended lessons and courses toward partial exposure to each lesson and eventually envision the acquisition of concepts such as:
Two points forming a line segment.
Understanding two intersecting lines and their properties.

What are the basic concepts of geometry?
Geometry is based on a small number of fundamental concepts which children need to learn:
Shapes: Recognizing geometric shapes such as circles, triangles and squares.
Dimensions: Processing the length of 2D shapes and depth of 3D shapes.
Angles: Identifying right, acute, and obtuse angles.
For instance: Opposite angles are equal when two lines intersect and the right angle measures 90°.
Measurement: Calculating area, perimeter and volume using geometry formulas.
Students can learn these elementary geometric postulates and approach problems involving closed shapes, parallel and line segments, and curves.
Comments
Your comment has been submitted