Quadrilaterals in Geometry: Types and Properties

Quadrilaterals fundamental concept in geometry, on which numerous mathematical issues and applied problems in the real world are founded. These four-sided polygons have four vertices and interior angles.

It is necessary to know the various types of quadrilaterals to understand the geometry of information (squares, rectangles, parallelograms, kites, etc). Characteristics include 360° interior angles, opposite angles, congruent sides, adjacent angles, and diagonal bisecting.

Quadrilaterals in Geometry are a fundamental concept, forming the basis for numerous mathematical problems and real-world applications. These four-sided polygons, with four vertices and interior angles, are integral to understanding geometric principles.

Understanding the types of quadrilaterals in geometry—such as squares, rectangles, parallelograms, and kites—is essential to mastering this topic. The properties of a quadrilateral in geometry include a total interior angle sum of 360°, opposite angles, congruent sides, adjacent angles, and diagonals that may bisect each other.

This article aims to present the idea of quadrilaterals, enumerate their features, their importance, and provide examples, so that one can grasp the idea of quadrilateral geometry and its potential use in various areas of study.

What are Quadrilaterals In Geometry?

The word "Quadrilateral" is taken from the Latin, "quadri" meaning with four corners, and "latus" meaning four sides.

Quadrilaterals in geometry are four-sided polygons with four angles. They are heterogeneous ensemble of different shapes such as squares, rectangles, parallelograms, and kites, with all of them possessing specific characteristics.

Relevant topics in the field of geometry include quadrilaterals, which are fascinating shapes characterized by unique properties. Quadrilaterals in geometry are defined as four-sided polygons where the sum of their internal angles always equals 360°. These shapes can have at least one pair of parallel sides or two pairs of parallel sides and angles that can be equal or different. Quadrilateral ABCD can have pairs of inverse sides, parallel sides, opposite sides, congruent in length, and so on.

Different Types of Quadrilaterals In Geometry

Quadrilaterals in geometry are subdivided based on their sides, angles, and symmetry. Understanding these categories helps in solving geometric problems efficiently. Below are the main types of quadrilaterals in geometry, each with unique characteristics and properties:

Trapezium

A trapezium is a quadrilateral with the property that there is one pair of opposite sides parallel. Its shape looks like a triangle with a slice out of the top, and two triangular slopes coming together at the edges, which are called bases. One set of opposite sides in a trapezium must be parallel to satisfy the conditions. The non-parallel sides are referred to as legs.

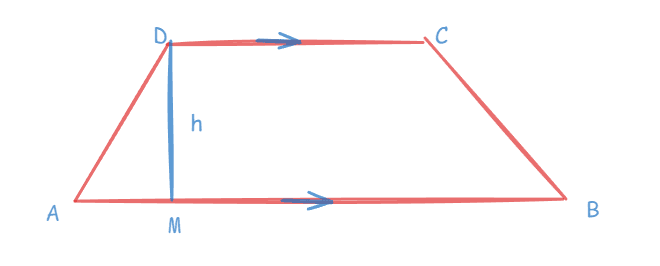
The above figure ABCD represents trapezium, h is the height and AB ,CD are parallel to each other and AD, BC are called legs.
Properties:

One pair of opposite sides is parallel.
Non-parallel sides can have equal length (isosceles trapezoid).
Angles adjacent to the parallel sides are supplementary.

Parallelogram

A parallelogram is a type of quadrilateral in geometry where opposite sides are equal in length, and two sides are parallel. Opposite angles are also equal, and the parallel sides are of equal measure. Parallelograms can be observed in the real world, such as on tilted bridges and diamond-shaped street signs.

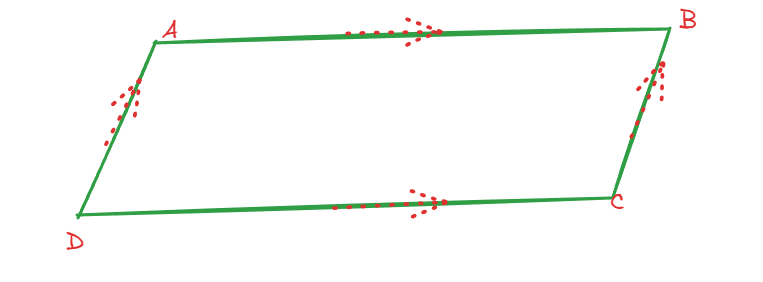
The above figure ABCD represents parallelogram, AB ,CD are parallel and AD , BC are also parallel to each other. Opposite sides are equal in length.

Properties:

Opposite sides are parallel and equal in length.
Opposite angles are equal.
Diagonals bisect each other(each diagonal cuts the other diagonal into two equal parts).
Adjacent angles are supplementary(the sum of angles equals to 180°).

Rectangle

A rectangle is a type of quadrilateral in geometry where the pairs of opposite sides are of equal length, and all four angles are right angles. The two diagonals of a rectangle divide it into two pairs of parallel sides with equal length. Additionally, all its angles measure 90°, and the opposite sides are parallel. Real-life examples of rectangles include books, screens, and tables.

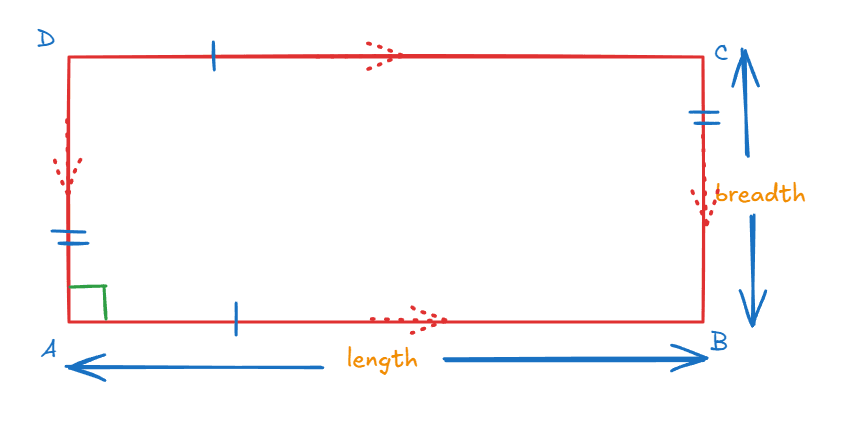
The above figure ABCD represents rectangle, AB ,CD are parallel and AD , BC are also parallel to each other. Opposite sides are equal in length and all the interior angles equal to 90°.

Properties:

All angles inside rectangle are 90°.
Opposite sides are of equal length.
Diagonals are equal and bisect each other.
Adjacent sides meet at right angles.

Rhombus

A rhombus is a type of quadrilateral in geometry, with all sides equal in length but internal angles not necessarily equal to 90°. The properties of a quadrilateral in geometry, like a rhombus, include diagonals that are perpendicular to each other and intersect at equal angles. The form of a rhombus can often be observed in kites and various types of jewels.

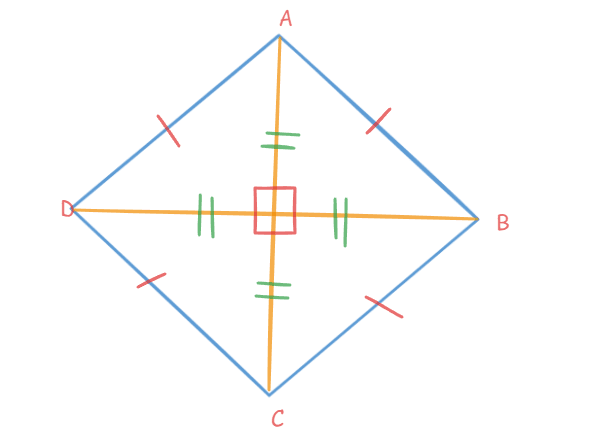
The above figure ABCD represents Rhombus. AC , BD are diagonals.

Properties:

All four sides are of equal length.
Opposite angles are equal.
Opposite sides of a rhombus are parallel to each other.
Diagonals bisect each other at right angles.
Adjacent angles are supplementary

Square

The square is a polygon that belongs to the types of quadrilaterals in geometry, characterized by all four sides of equal length and four right angles. Among the properties of a quadrilateral in geometry, the square's diagonals are notable as they bisect each other at right angles and are equal in length. Squares are common in real life, seen in tiles, chessboards, and windows.

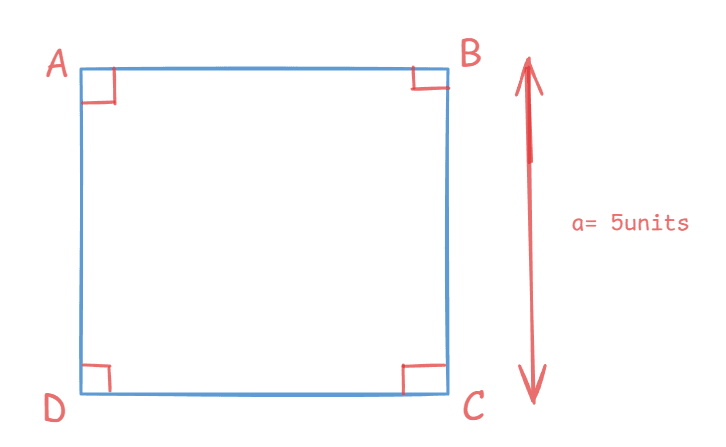
Properties:

All sides are equal in length.
Four right angles.
Diagonals bisect at right angles.
Diagonals are of equal measure.

Kite

A kite is a polygon where the sides opposite each other are congruent and isomorphic to each other (i.e., of equal length). In the diagonals of a kite, the angle of intersection of the two diagonals made of opposite sides equal the kite is a right angle and one of the diagonals splits its opposite diagonal in half.

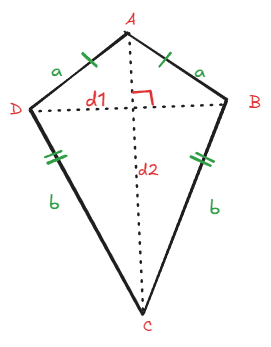
The above figure ABCD represents kite. AD, AB are of same length and CD, CB are also same length. d1, d2 are diagonals of kite.

Properties:

Two adjacent sides are of equal length.
Diagonals intersect at right angles.
One diagonal bisects the other.

Area and Perimeter of Quadrilaterals

The area of the quadrilateral is the total space occupied by four points on the figure.

The perimeter of a quadrilateral is the total distance around its four sides. To find the perimeter, simply add up all four sides.
E.g.: ABCD is a quadrilateral, its perimeter is the sum of the lengths of four sides: AB, BC, CD, and DA.

Perimeter = AB + BC + CD + AD

Quadrilateral	Area	Perimeter
Square	A= a *a	P=4a
Rectangle	A=l×w	P=2(l+w)
Parallelogram	A=b×h	P=2(a+b)
Rhombus	A=1/2 (d1 * d2)	P = 4a
Trapezoid	A= 1/2 (b1+b2)*h	P = a+b1+b2+c
Kite	A= 1/2 (d1* d2)	P = 2(a+b)

Where,

a and b represent the lengths of the sides.
l represents the length and w represents the width.
b1 and b2 represent the lengths of the parallel sides of the trapezoid.
h represents the height.
d1 and d2 represent the lengths of the diagonals
a, b1, b2, and c are the lengths of the sides of the trapezoid.

Properties of Quadrilaterals In Geometry

Properties of quadrilaterals simplifies solving problems:

Interior Angles: The sum of all interior angles is 360°.
Opposite Sides: Opposite sides can be parallel, equal in length or both.
Diagonals: Dividing into their respective diagonals, they are the same length, or they make an angle of 90°.
Adjacent Angles: Adjacent angles in parallelograms are supplementary.
Right Angles: Rectangles and squares have four right angles.
Equal Length Sides: Rhombuses and squares have sides of equal length.
Pairs of Parallel Sides: Parallelograms, rectangles, and squares have two sets of parallel sides.

Quadrilateral Examples

Quadrilaterals are not just abstract objects, they have practical uses in several fields:

Architecture: Quadrilaterals are the foundation for structural designs, including windows and tiles, which are often such that their faces are parallel and the angles are equal.
Urban Planning: The shapes of the quadrilateral are applied into garden, plot, road, etc., and make effective utilization of limited space, as well as visually harmonious formations.
Computer Graphics: Quadrilaterals are among the most important tools for the design and the deformation and surface treatment of digital design and animation meshes of 2D and 3D meshes of design models.
Interior Design: Quadrilaterals represent the geometry that supports the design of furniture in general, but especially tables, chairs and cabinets, so that they have the appropriate ease of use and esthetic.
Geology: Quadrilateral meshes are employed in cartography and land surveys to deliver correct size and distance of the earth's surface.

Practice Questions on Quadrilateral

Define the geometry of a quadrilateral in a way that one pair of oppositely oriented sides is parallel and opposing sides are of equal length.
Diagonals of a parallelogram passing through them are universally known geometric features. On the other hand, although there is a not so likely, and perhaps, may not be applicable in this case, some possible possibility of proof by mathematical means for this property is there.
Draw a kite and mark its diagonals. Prove that the diagonals intersect at right angles.
The quadrilateral having all sides of equal length and all angles equal to 90° is referred to as a square.

Overview of Quadrilaterals, their characteristics and real-life examples

Quadrilateral	Definition	Real-Life Examples	Figures
Square	The square is the polygon having four equal sides and four acute angles. All its angles are 90 degrees. Diagonals are bisected by them at right angles, and also have equal lengths.	Tiles, chessboards, windows
Rectangle	The rectangle is a quadrilateral with sides of equal length opposite one another and the four corners with right angle. Diagonals' lengths are the same and diagonals cross each other. The opposite sides are parallel.	Smartphones, door frames, notebook covers
Parallelogram	A parallelogram is a closed figure having two opposite edges of the same length and laying on the same parallel line. Opposite angles are congruent and diagonals bisect one another.	Flat surfaces of tables, desks
Rhombus	A rhombus (also equilateral quadrilateral/diamond) is a quadrilateral in which all four sides equal each other. Opposite sides are parallel, and opposite angles are equal.	Diamond-shaped road signs, the diamond on a deck of playing cards
Trapezium	A trapezium is a polygon having two opposite sides of the polygon parallel. The two congruent sides are also known as bases, while non-congruent sides are known as legs.	Designs of bridges, certain handbag shapes
Kite	A kite is a quadrilateral, in which two opposite side pairs are of equal length. Its diagonals are cut 90 degrees at their intersection and one diagonal bisects the other.	Kites for flying, decorative designs

Quadrilaterals In Geometry - FAQs

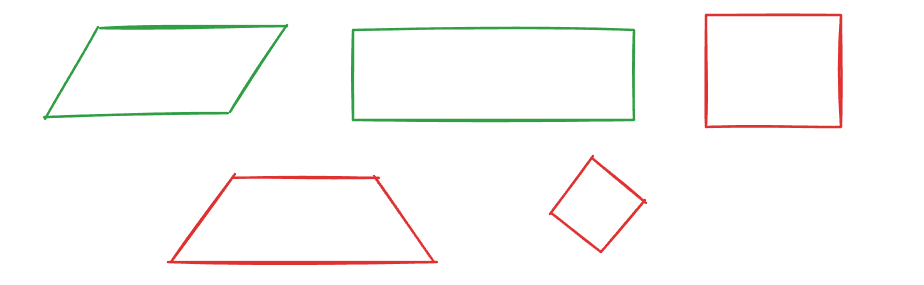
How many Types of Convex Quadrilaterals are there?

Convex quadrilaterals in geometry include five types:

Trapezium, parallelogram, rectangle, rhombus, and square. Each of these convex quadrilateral has distinct properties.

parallelogram, rectangle, square, trapezium, rhombus

Which quadrilaterals in geometry has four congruent sides?

Rhombus and square are known to have four equal sides.

In a rhombus, the diagonals intersect at right angles and the opposite angles are equal.

In a square, all sides are of same length, with four right angles.

What kind of quadrilaterals in geometry has 4 equal sides and 4 right angles?

A square is the only quadrilateral that meets both criteria of having four equal sides and four right angles. Its diagonals cross at right angle and each diagonal cuts the square into two identical triangles. All the interior angles and angles of a square are the same.

Important properties of squares:

The opposite sides are parallel.
All four angles are equal and equal to 90°.
Both diagonals bisect each other at 90°.

Do kites have parallel sides?

No, kites do not have parallel sides. They have two pairs of adjacent sides that are at equal angles. The two equal side opposite angles are equal. Kites are special since their diagonals meet at right angles forming a unique quadrilateral.

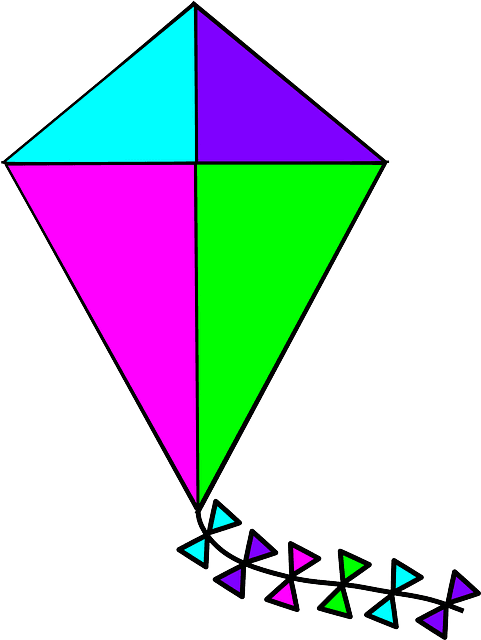
Unlike parallelograms or trapezoids, there are no counterparts of opposite sides that are parallel. This special feature allows kites to be easily distinguished from other quadrilaterals.

What is the Sum of the Interior Angles in a Quadrilateral?

The total sum of all the angles of any quadrilateral is always 360° degrees. This is one of the basic characteristics of all quadrilaterals, whether they are simple ones (squares and rectangles) or complex ones (trapezoids and kites).

The degree of interior angles may be different but the sum of all interior angles equals 360°. This is key for recognizing and classifying complex quadrilaterals. It is fixed for any given shape of the quadrilateral.

What are the Common Properties of all quadrilaterals in geometry?

Common properties of a quadrilateral in geometry include having four sides, four vertices, four angles, and an interior angle sum of 360°. Moreover, quadrilaterals in geometry can be classified according to side length, angle, and parallel sides.

For instance:

Squares and rectangles possess opposite sides of equal length and parallel and all four angles are acute.

Parallelograms have opposite sides which are parallel and have the same length, and opposite angles which have the same value.

Trapezoids have only one pair of opposite sides that are parallel.

Kite has two pairs of adjacent sides that are equal in length. Their diagonals intersect at right angles (90°) and one diagonal bisects the other.

How to find the perimeter of a quadrilateral?

The total length of all four edges gives the perimeter of the quadrilateral.

Example: A rectangle has a length of 5cm and width of 8cm, its perimeter will be:

P = 2*(5 + 8) = 26 cm

For any quadrilateral, the lengths of all four sides are summed together:

P = a + b + c + d Where a, b, c, and d are the respective lengths of the sides.

What is the name of that quadrilateral whose all angles measure 90°, and the opposite sides are equal?

This quadrilateral is known as a rectangle. In the types of quadrilaterals in geometry, a rectangle is defined by its unique properties. It has all four angles equal to 90° (right angle), and the two opposite sides are equal in length and parallel. Rectangles are a particular kind of parallelogram and share some properties of a quadrilateral in geometry with squares. However, unlike a square, any of the sides in a rectangle may not be of equal length (only the opposite sides will be the same length).

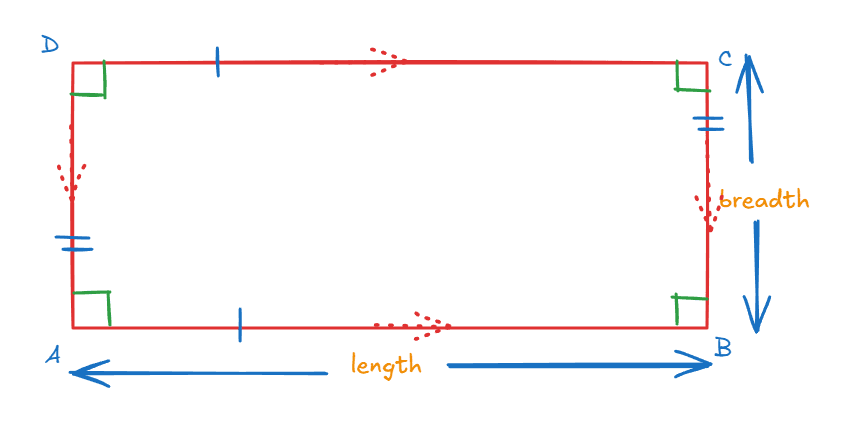
This results in rectangles, one of the most popular and widely used types of quadrilaterals in geometry, with applications ranging from architectural design to the common objects around us.

Can all the angles of a quadrilateral be acute?

No, the sum of the angles of a quadrilateral cannot be acute. In a quadrilateral, the sum of the interior angles is always 360°. An acute angle is less than 90°, and the sum of four acute angles cannot be 360°.

For example, in a convex quadrilateral, at least one angle has to be obtuse to fulfil this total. This property is valid for each type of closed shape of quadrilateral(regular or irregular).

Quadrilaterals in Geometry: Types and Properties